Atcoder 试题乱做 Part 3
难度标签:$\color{red}\texttt{[HARD]}$,$\color{blue}\texttt{[NORMAL]}$,$\color{green}\texttt{[EASY]}$。
[AGC007C] Pushing Balls
$\color{blue}\texttt{[NORMAL]}$
神秘题。
考虑一个球被吃掉之后的情况:坑会少一个,球也会少一个,所以仍然是 $n+1$ 个坑,$n$ 个球的形式。
我们考虑两个关键点之间的距离数组 $\{d_i\}$,那么经过一次推球,其变化应是:一个长度为 $3$ 的连续段进行合并。于是,$d_i$ 的变化有以下两种:
- 在 $d_i$ 之前的段合并了,导致 $d_{i+2}$ 替换了 $d_i$。
- 正好合并当前部分,变成 $d_i+d_{i+1}+d_{i+2}$。
计算可得:
$$ d'_i=d_i+\dfrac{i\times (d_{i+2}-d_i)+(d_{i+1}+d_{i+2})}{2n}=d_i+\dfrac{i\times 2x+2d_i+5x}{2n} $$
发现仍然是一个等差数列!于是模拟上述过程即可。至于一轮的期望移动长度,就是所有 $d$ 的平均数。时间复杂度 $\mathcal{O}(n)$。
[AGC007F] Shik and Copying String
$\color{blue}\texttt{[NORMAL]}$
首先,每个字符到达他应该在的位置,其过程可以描述为一条路径。由于要求最小步数,贪心地想,每个位置一定找最近的可以匹配的位置。从另一个角度,这样也是对的:因为位置越近,影响到的点就越少,对别人的移动的影响就越小。
同时,下标递增,选取的位置也应该不降,否则就会出现交叉从而无解。于是,一个简单的方法是从后往前依次确定每个点的取值位置。同时,每条路径应该是每次尽量向右移动,动不了了才考虑向下移动。
考虑如何计算总共需要多少次操作,注意到就是所有路径中,转折最多的一条的转折个数。于是现在的问题就是维护每一条路径的转折个数,可以从后往前扫描,用队列维护转折位置,注意到一部分转折点会向左下移动一步,一部分会被弹出,可以用队列维护。
时间复杂度 $\mathcal{O}(n)$。
[AGC012C] Tautonym Puzzle
$\color{blue}\texttt{[NORMAL]}$
注意到长度为 $200$,字符集是 $100$,这提示我们将序列划分为前后两部分,保证所有合法子序列都跨过前后两部分。
一个简单构造方法是将后半段设置为 1 2 3 4 ... 99 100,则前半段只需要构造一个序列,其中所有上升子序列都有一个贡献即可。
考虑从小到大在前半段插入元素,当前元素插入在所有元素左侧,答案个数 $+1$;插入在所有元素右侧,答案个数 $\times 2+1$。注意到这类似二进制构造,按照这个策略就可以做到 $2\log n$ 左右的长度。
[AGC012B] Splatter Painting
$\color{blue}\texttt{[NORMAL]}$
麻了,被 B 题教育了/ll
注意到 $d\le 10$ 这个关键条件,从这方面开始思考。首先,对于点 $x$ 的两次操作 $(d_1,v_1,t_1),(d_2,v_2,t_2)$,其中 $t$ 是其修改时间,若 $d_1<d_2,t_1<t_2$,则 $1$ 是完全没用的。于是对于一个点 $x$,与固定的 $d$,只需要保留 $t$ 最大的修改即可。
同时,注意到如果 $x\to y$,则 $(x,d)\to (y,d-1)$,所以可以设 $f(x,d)$ 表示从 $x$ 开始,对于固定的 $d$ 的最后一个修改,然后每次从 $f(x,d)$ 更新 $f(y,d-1)$。
时间复杂度 $\mathcal{O}(d(n+m))$。
[AGC012D] Colorful Balls
$\color{green}\texttt{[EASY]}$
首先,同色球之间的交换并不改变序列颜色,于是,每次如果要交换两个元素,可以先把他们尝试换成重量尽量小的同色元素,然后再进行交换。
于是,对于两个同色点,可以先将权值较大的换成权值较小的,与其他球进行一次交换,然后将两个同色球换回来,就相当于直接拿权值大的和别的球交换了。
因此,当一个球能够与同色球中权值最小的球进行交换,我们就可以认为这个球的权值就是同色球中的 $\min$。
容易看出,这样修改一下之后,同色球之间交换的意义就全部榨干了。现在只需要考虑异色球之间的交换。
使用类似的想法,要交换两个位置 $x,y$ 的时候,首先找到颜色异于 $x$ 的,权值最小的球 $z$,交换过去,如果 $z$ 与 $y$ 颜色不同,则完成了交换;否则,找到异于 $y,z$ 的最小球,再换一换也可以完成 $x,y$ 的交换。
于是,当一个球能与“和自己不同色的最小权值球”进行交换,则可以说明他可以与其他满足这个条件的任意球互换。
因此只需要记录最小权值球、“与最小权值球颜色不同的,最小权值球”,就可以得到每种颜色有多少个球可以随意互换。最后就是一个组合数,复杂度 $\mathcal{O}(n)$。
[AGC012E] Camel and Oases
$\color{blue}\texttt{[NORMAL]}$
首先,显然只有 $\mathcal{O}(\log V)$ 种 $V$ 的取值。每次一定会走到一个联通块,然后把这个极长的连通块都走完。
因此,可以建立一张 $\mathcal{O}(\log V)$ 层的图,每层将节点划分成若干区间。则现在只需要在每层中选一个节点,然后覆盖全体即可。
由于只有 $\mathcal{O}(\log V)$ 层,$V$ 却只有 $2\times 10^5$,所以从值域上考虑。不妨直接状压,设 $\text{dp}_S$ 表示已经用了 $S$ 这些层,从左端点开始最远能延申到哪里。
现在再来考虑如何输出从每个点开始的结果,相当于钦定了第一层在哪个区间。可以通过枚举区间左侧、右侧分别用了哪些层,然后做一个类似二维数点的东西。
时间复杂度 $\mathcal{O}(n\log V+V)$。
[AGC013C] Ants on a Circle
$\color{blue}\texttt{[NORMAL]}$
经典结论是可以把掉头看作穿过,然后就可以快速得到蚂蚁最后在哪些位置,只是不知道对应关系而已。
注意到由于相撞会掉头,所以相对顺序是不变的。意味着只需要找到 $1$ 的位置,所有位置都确定了。
如果是在数轴上,则最左侧的就是 $1$。但现在在环上,当一个人顺时针经过 $0$,可以认为 $1$ 前面多了一个人;一个人逆时针经过 $0$,可以认为是 $1$ 前面少了一个人。所以只需要计算每个人穿过 $0$ 的次数即可。
时间复杂度 $\mathcal{O}(n)$。
[AGC013D] Piling Up
$\color{blue}\texttt{[NORMAL]}$
首先集合内的总球数不变,因为每次拿出去 $2$ 个,拿进来 $2$ 个。
所有操作可以看作以下四种:
- 集合中至少有一个 $0$,往序列后加一个 $01$,集合内元素不变。
- 集合中至少有一个 $0$,往序列后加一个 $00$,集合内一个 $0$ 换成一个 $1$。
- 集合中至少有一个 $1$,往序列后加一个 $10$,集合内元素不变。
- 集合中至少有一个 $1$,往序列后加一个 $11$,集合内一个 $1$ 换成一个 $0$。
这就很像一个格路计数的内容,相当于从 $x=0$ 走到 $x=m$,不跨过 $y=0$ 和 $y=n$。其中 $y$ 一维表示有多少个 $0$。直接考虑 $\text{dp}$:设 $\text{dp}_{i,j}$ 表示已经填了 $i$ 次,还有 $j$ 个 $0$ 的方案数。
但是这样会存在算重的情况,因为一组路径可能在多个起点被计算到(即路劲可以在限制内平移):
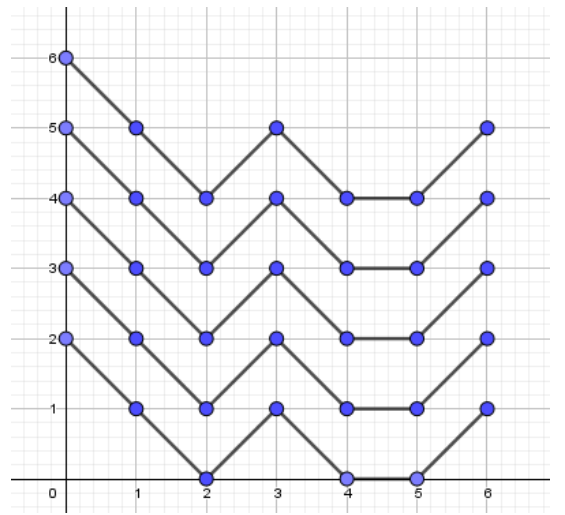
一个钦定方法就是钦定路径必须至少经过一次边界,这样几乎所有路径都会被限制。只有一些恰好在起点碰到 $y=0$,终点不碰到 $y=n$ 的一些直线,可能被计算两次。不过可以将限制改为 “必须要从边界上再进行一次操作”,这样所有路径都只会恰好算到一次了。
$\text{dp}$ 设置成 $\text{dp}_{i,j,0/1}$ 表示已经填了 $i$ 次,还有 $j$ 个 $0$,是否在边界上进行过操作的方案数就行了。时间复杂度 $\mathcal{O}(nm)$。
[AGC014E] Blue and Red Tree
$\color{green}\texttt{[EASY]}$
显然,在连了一条红边之后,树可以看作被划分成两个连通块,剩下的路径必须在不同的连通块中。
于是,每次考虑选择一条路径,满足这条路径上存在一条边,使得只有这条路径经过这条边。然后断掉这条边,继续操作。
树剖维护即可,容易发现当某一时刻不存在上述情况则无解。时间复杂度 $\mathcal{O}(n\log^2 n)$。
[AGC014B] Unplanned Queries
$\color{green}\texttt{[EASY]}$
被洛谷评分吓到了,导致掉智严重
考虑合法的一个必要条件:每个点的度数都是偶数。一条路径,中间的点度数都 $+2$,只有两个端点只 $+1$。如果端点的度数不是偶数显然无解。否则构造一条链就一定合法了。时间复杂度 $\mathcal{O}(n)$。