题目链接: CF1139C Edgy Trees

第一次CF修仙就遇到了这样的神题

行吧 其实也不是很难

题意大概就是让你找出一棵有$n$个点的边带色的树上，依次经过 $k$ 个点，并且该路径是一条好的路径的这 $k$ 个点分别有多少组，好的路径当且仅当这条路径至少经过一条黑边($ps$：可以重复经过同一个点 甚至可以呆着不动)

注意，同一路径上的点不一定直接相连，但一定要联通！

语文不好 题意讲错了别怪我 还是去看题比较靠谱

这就是树的好处了，两个点之间有且只有一条简单路径

讲一下我比赛时候的思路吧（以下均用好路、坏路表示好的路径和不好的路径，“长度为 $k$ 的路径”表示经过 $k$ 个点的路径）

首先，先看懂题目 百度翻译，看到 $n <= 10^5$，瞬间慌张 主要是发现不能暴力乱搞

然后，可以发现要保证每条路径上至少有一条黑边，很难用一些效率高的算法维护 可能是我太菜了不会做

所以考虑反方向思考，找出所有的坏路，拿路径总数去减去坏路个数，就可以得到好路的个数了

建议往下看之前，先把几个样例想明白

首先，很快就可以得到：路径总数 $= n^k$，因为可以随便枚举 $k$ 个点

然后就是怎么求坏路个数了

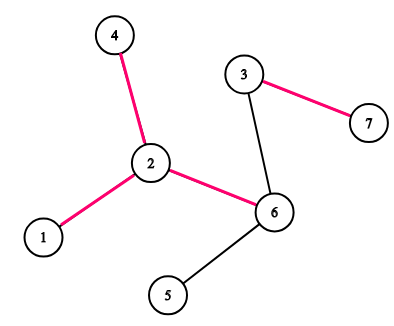
这是原图

怎么样才能求出坏路呢？也就是如何才能使得路径上的点的整个过程中没有黑边

那就把黑边删掉

其实思路是对的

当我们把上面的图中所有的黑边全部去掉，会变成这个样子

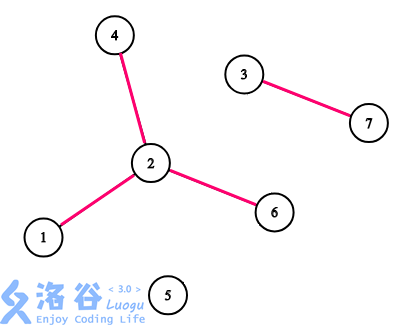
不难发现这棵树变成了几个联通块，并且块内不存在黑边和环

那么，很快就能够发现设一个联通块内的点数为 $x$ 的时候，长度为 $k$ 的路径一共 $x^k$ 个，并且这些路径，全部都是坏路！（因为整个联通块中间没有黑边，所以在联通块中无论如何选择，路径上都不可能有黑边 太显然了）

所以，我们的思路就确定啦，分别求出所有路径个数和每个红边联通块中的路径个数，相减即可

那么，怎么维护红联通块内点的个数呢

显然是 冰茶几 并查集

最后再乱搞，加一个快速幂

复杂度不会算，应该还是比较快的 我太弱了

Code ：

//Code By CXY
#include<bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 10;
const int mod = 1e9 + 7;

#define ll long long//记得开long long！！

ll n,k,ans;
ll cnt[MAXN];
ll f[MAXN];

ll find(ll x) {
    if(x == f[x]) return x;
    return f[x] = find(f[x]);
} //简单并查集，没啥解释的

void unity(int x,int y) {
    if(find(x) != find(y))
        f[find(x)] = find(y);
} //并查集合并操作

ll qpow(ll a,ll b) {
    ll res = 1,base = a;
    while(b) {
        if(b & 1) (res *= base) %= mod;
        (base *= base) %= mod;
        b >>= 1;
    }
    return res;
} // 快速幂

int main () {
    cin >> n >> k;
    for(int i = 1;i <= n; ++i)
        f[i] = i; //并查集初始化
    for(int i = 1,x,y,col;i < n; ++i) {
        cin >> x >> y >> col;
        if(col == 0) unity(x,y);//如果是红边，就合并，就可以得到红联通块 
    }
    for(int i = 1;i <= n; ++i)
        cnt[find(i)]++; //每一个并查集中间祖先的cnt中记录整个联通块中点的个数
    for(int i = 1;i <= n; ++i)
        if(f[i] == i) (ans += qpow(cnt[i],k)) %= mod;//如果这是一个新的联通块，就加上cnt[i]^k
    cout << (qpow(n,k) + mod - ans) % mod << endl; //最后用总数减去所有联通块内路径的和，记得取模！！还有注意负数的情况
    return 0; //华丽地结束
}

初二的$OIer$，请多关照