【学习笔记】压缩后缀自动机
前言
群友一部分会,一部分人自己编出来了,但是我不会也编不出来/ll
本学习笔记基本参考:
【IOI2020 论文集】徐翊轩,浅谈压缩后缀自动机 。
定义
对于字符串 $S$ 的子串 $S_{l,r}$:
定义其上文 $\text{LeftContext}(S_{l,r})$ 为最长的,每次 $S_{l,r}$ 出现,则一定会接在 $S_{l,r}$ 前面一起出现的部分(即 $\text{SAM}$ 上同一个节点上的最长串);
定义下文 $\text{RightContext}(S_{l,r})$ 为最长的,每次 $S_{l,r}$ 出现,则一定会接在 $S_{l,r}$ 后面一起出现的部分(即反串 $\text{SAM}$ 上同一个节点上的最长串)。
则显然有:
$$ \text{LeftContext}(\text{RightContext}(S_{l,r}))=\text{RightContext}(\text{LeftContext}(S_{l,r})) $$
于是:
设上下文 $\text{Context}(S_{l,r})$ 为:
$$ \text{LeftContext}(\text{RightContext}(S_{l,r})) $$
即总是和 $S_{l,r}$ 一同出现的极长串。注意到根据 $\text{LeftContext}$ 和 $\text{RightContext}$ 的定义,串 $T$ 在 $\text{Context}(T)$ 中的出现位置是唯一的。
定义左集合 $\text{Left}(S_{l,r})$ 表示 $S_{l,r}$ 所有出现位置的左端点集合(反串 $\text{SAM}$ 的 $\text{endpos}$ 集合);
定义右集合 $\text{Right}(S_{l,r})$ 表示 $S_{l,r}$ 所有出现位置的右端点集合($\text{SAM}$ 的 $\text{endpos}$ 集合)。
传统后缀数据结构
后缀字典树
就是把所有后缀插到 $\text{trie}$ 上。例如 $\tt{abaab}$ 的后缀字典树就是:
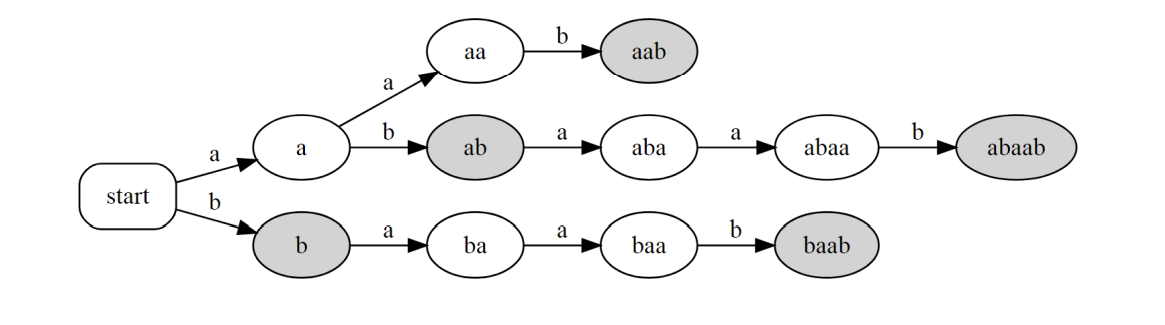
后缀自动机
其实本质上就类似将后缀字典树进行最小化,把所有 $\text{Right}$ 集合相同的节点合并。$\tt{abaab}$ 的后缀自动机是:

后缀树
本质就是将后缀字典树进行收缩,即建立叶子节点的虚树,或者说压缩所有只有一个儿子的节点。$\tt{abaab}$ 的后缀树是:
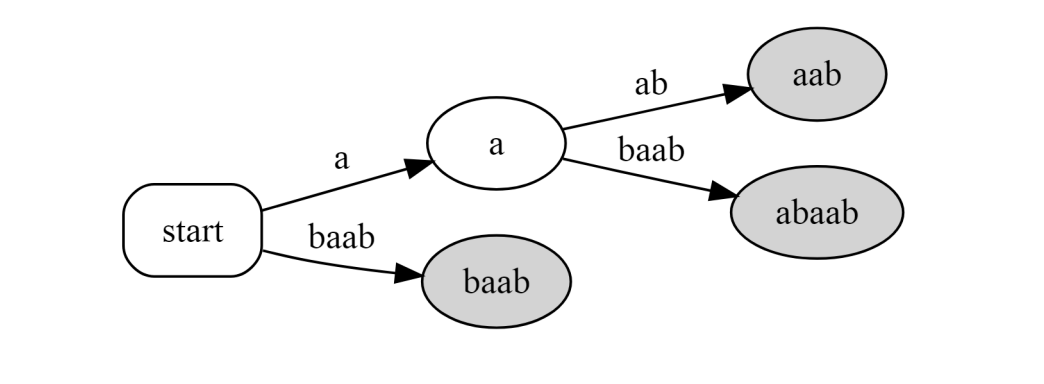
不过发现直接这样会吃掉一些代表后缀的点,但是我们可能需要用。所以把定义改成:建立所有代表原串后缀的节点的虚树,这样得到的我们称作完整后缀树。$\tt{abaab}$ 的完整后缀树是:
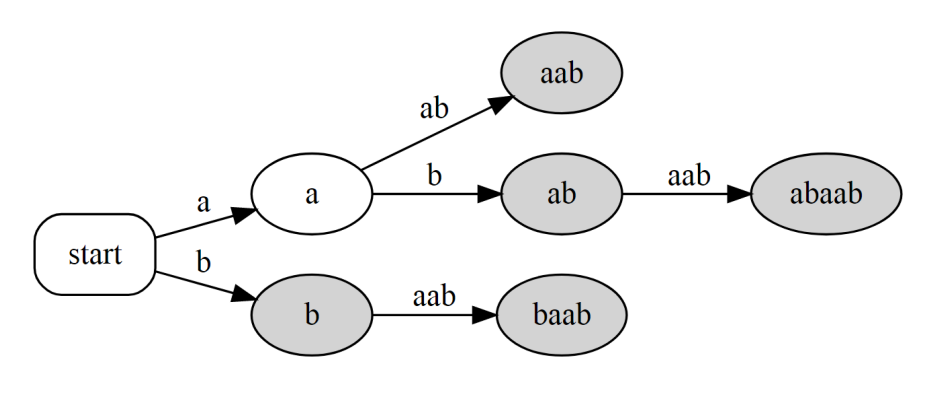
后缀树不能称作 $\text{DFA}$。
压缩后缀自动机
定义
后缀字典树,进行最小化会得到后缀自动机,进行收缩会得到后缀树。同时进行最小化和收缩,就会得到压缩后缀自动机。
$\tt{abaab}$ 的压缩后缀自动机是:
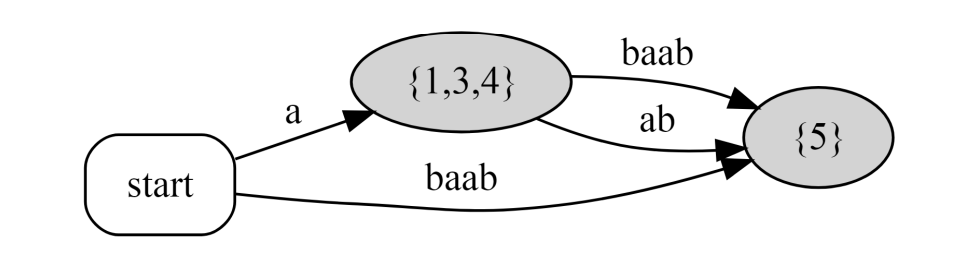
即把后缀自动机上,所有出度为 $1$ 的点缩起来;或者把后缀树上,所有 $\text{Right}$ 集合相同的节点缩起来。
而对完整后缀树进行最小化操作,得到的是完整压缩后缀自动机。$\tt{abaab}$ 的完整压缩后缀自动机是:
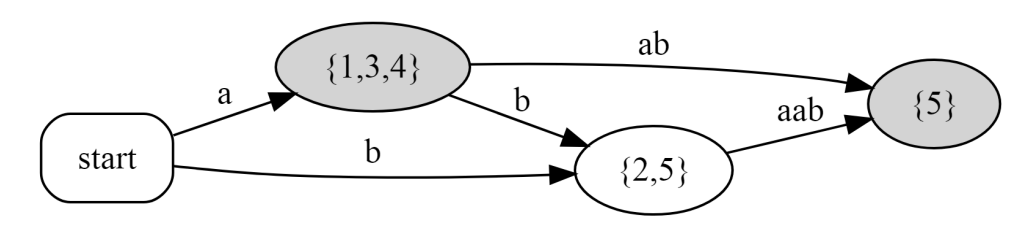
构建方式
既然压缩后缀自动机是对后缀字典树做最小化与收缩之后得到的结果,那自然有两种角度:先最小化,或先收缩。
我们选择先进行最小化,即先求出后缀自动机,然后进行收缩。首先将后缀自动机上所有出度不为 $1$ 的点标记为灰色,然后找到每个灰色点在 $\text{DAG}$ 上的下一个灰色点,将其中所有边进行压缩即可。
注意到一个灰色点往后遇到的第一个灰色点一定是唯一的,因为中间的点都是 $1$ 度点。于是可以在 $\mathcal{O}(|S|)$ 的时间内建立压缩后缀自动机。
再考虑完整后缀自动机,此时没有与之对应的后缀自动机来直接收缩了。不过,注意到完整后缀树与后缀树的差别,只有作为后缀的节点同样被染灰,所以只需要将后缀自动机上代表后缀的节点也设为灰色,再做与上面一样的操作即可。复杂度也是 $\mathcal{O}(|S|)$。
性质
压缩后缀自动机上节点 $i$ 的所有入边上的字符串,都是 $i$ 代表的最长串的后缀。
显然。
设 $L_i$ 表示压缩后缀自动机上节点 $i$ 的入边中,最长边的长度,则:
$$ \sum L_i=\mathcal{O}(|S|) $$
这是因为,一个灰点往后的最近灰点是唯一的,容易证明每条原后缀自动机上的边,在压缩后缀自动机的 $\sum L_i$ 上至多产生 $1$ 的贡献。
而又因为第一条性质,所以可以把 $i$ 号点的所有入边,描述为 $i$ 号点的最长入边的后缀,从而维护一些信息。
对称压缩后缀自动机
定义
对于一个后缀自动机,我们可以用一个节点上的最长串来表示他。例如 $\tt{abaab}$ 的后缀自动机可以表示为:

可以看作后缀自动机保留了所有 $\text{LeftContext}(T)=T$ 的子串 $T$ 对应的节点。
考虑我们在构造完整压缩后缀自动机的时候,出度为 $1$,且 $\text{Right}$ 不包括 $|S|$ 的所有节点,即只有唯一出边,且不是原串后缀的节点,全部被缩掉了。这样的串恰恰满足:
$$ \text{RightContext}(T)\ne T $$
也就是说,完整压缩后缀自动机上,只有 $\text{LeftContext}(T)=\text{RightContext}(T)=T$ 所代表的节点被保留了,即 $\text{Context}(T)=T$。
于是一个串的完整压缩后缀自动机,可以通过满足 $\text{Context}(T)=T$ 的子串来描述每个节点。例如 $\tt{abaab}$ 的完整压缩自动机可以描述为:
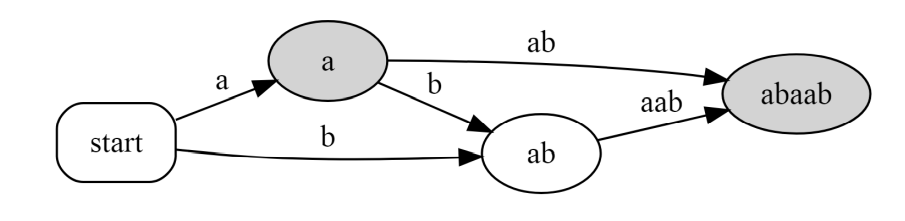
注意到,满足 $\text{Context}(T)=T$ 的子串,在反串 $S'$ 上与一个满足 $\text{Context}(T')=T'$ 的子串一一对应。
于是,我们可以将正串、反串的完整压缩后缀自动机建立在一起,公用节点,保留两套转移边。
同时对字符串的正反串建立完整压缩后缀自动机,将对应的节点合并,并同时保留两组转移边,称得到的结果为对称压缩后缀自动机。
例如 $\tt{abaab}$ 的对称压缩后缀自动机为:
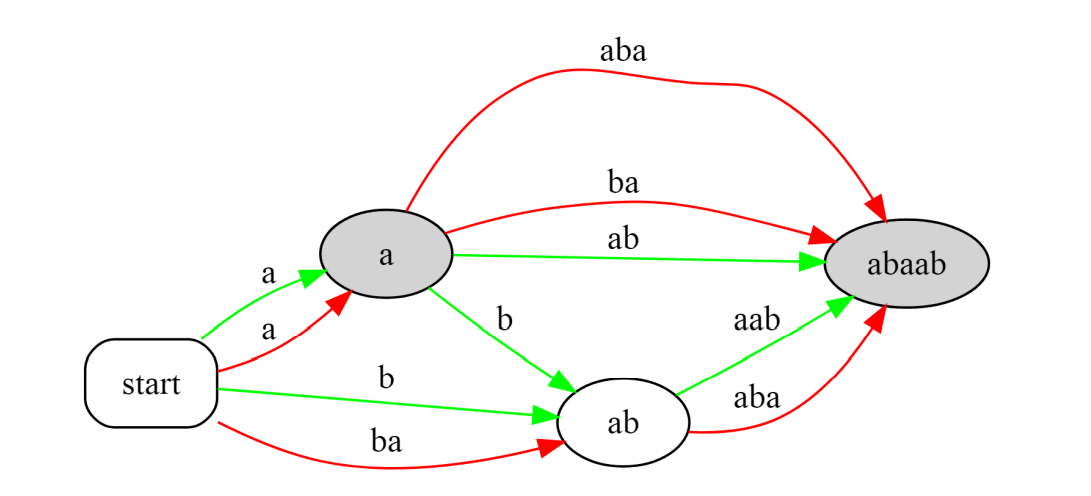
其中绿色的是原串的转移边(在后面加字符),红色的是反串的转移边(在前面加字符)。
构造方式
对正串、反串分别建立完整压缩后缀自动机,然后就只需要找一一对应关系了,容易通过 $\text{Hash}$ 等方式实现。
or2
orz
orcxy