Atcoder 试题乱做 Part 2

难度标签：$\color{red}\texttt{[HARD]}$，$\color{blue}\texttt{[NORMAL]}$，$\color{green}\texttt{[EASY]}$。

[AGC007D] Shik and Game

$\color{blue}\texttt{[NORMAL]}$

之前做过一道有点像的 CF 题，结果又冲了一发贪心

考虑 $\text{dp}$，设 $\text{dp}_i$ 表示走到 $i$，解决前面所有点最少需要多少步。则：

$$ \text{dp}_i = \min\{ \text{dp}_j + x_i-x_j+\max(T, 2(x_i-x_{j+1}))\} $$

由于距离递增，所以后面的 $\max$ 可以用一个指针来维护，把式子拆一下维护一些 $\min$ 就行了。复杂度 $\mathcal{O}(n)$。

[AGC006F] Blackout

$\color{red}\texttt{[HARD]}$

偷看题解第一句话

首先，这个东西就是一张图，$(x,y)$ 被染黑当且仅当 $x\to y$，则他的意思是如果出现 $x\to y\to z$，则出现三元环 $z\to x$。

题解第一句话：考虑三染色。

顺着这个思路向下，将点分为 $A,B,C$ 三类，我们希望只存在 $A\to B, B\to C,C\to A$ 的边。手玩一下，猜想对于一个连通块，如果能被这样成功三染色，则会生成一个“三分完全图”状物。即所有 $A$ 类向所有 $B$ 类连边等。

可以归纳证明，大概是考虑加入一条新边之后的变化。也可以和我一样做得很麻烦 保留一棵生成树，然后归纳证明树上任意深度 $\bmod 3$ 不同的点之间都存在边。

继续考虑，如果不能这样成功三染色，说明有边不满足这样的条件。继续考虑生成树，说明要么是不同深度 $\bmod 3$ 的点之间出现了反向边，要么是同深度 $\bmod 3$ 的点之间连边了。可以发现任意一种情况都会出现一个二元环。二元环的出现意味着自环的出现，自环会引出与这个点相关的所有边，从而所有边都存在了。故这种情况下，连通块是完全图。

当然，如果这张图可以被三染色，但是三种颜色不都被使用到了，则只有原图上的边会出现。

时间复杂度是 $\mathcal{O}(n)$。

[AGC008E] Next or Nextnext

$\color{blue}\texttt{[NORMAL]}$

首先肯定要化成环的形式。考虑每个点留下一个出边的时候会有哪些情况。

每一个点都指向下一个点，则环不变：

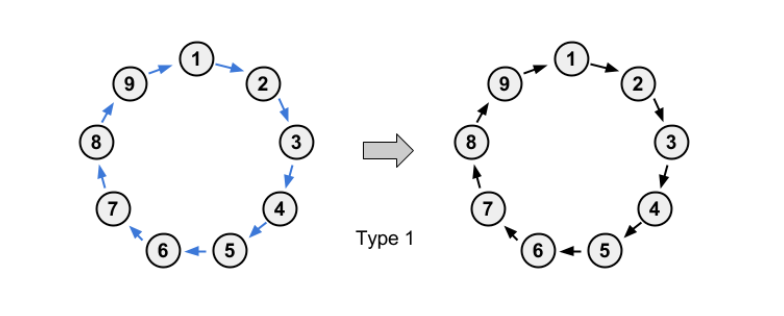
每一个点都指向下下个点，且环大小是奇数，还是一个环：

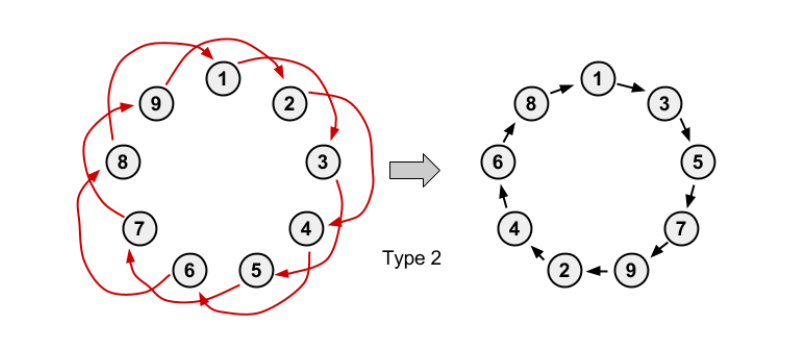
每一个点都指向下下个点，且环大小是偶数，变成两个大小一样的环：

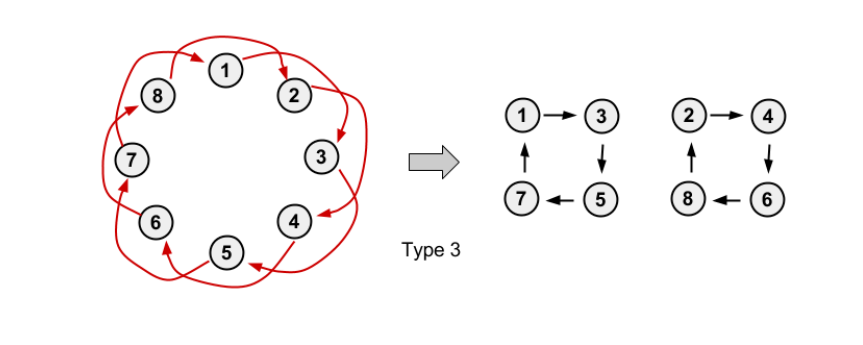
一部分指向下一个，一部分指向下下个，变成基环树：

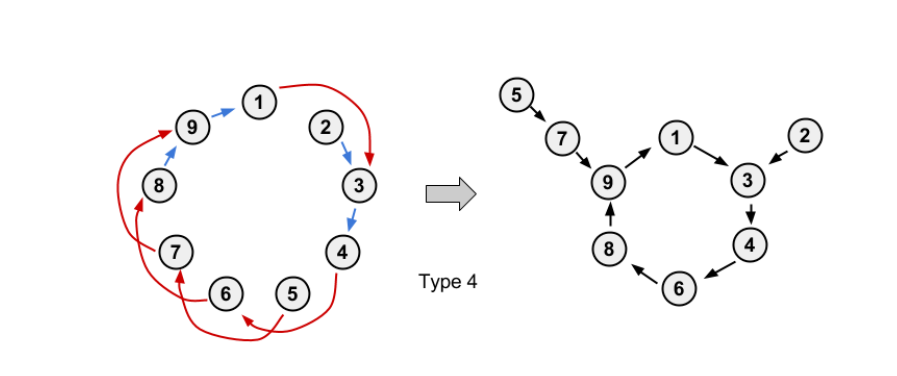
前三种是简单的。关键在于第 $4$ 种，注意到这个基环树有一些特点，例如他除了环之外的部分都是一些链，且一个环上点至多连出一条链。这个规律的说明方法大概可以先连出环，将环上的点不在图中的边删去，这样就会剩下一些链，然后这些链只不过有可能接到别的环上点，或接到下一个链的末尾。

注意到对于第 $4$ 种情况：

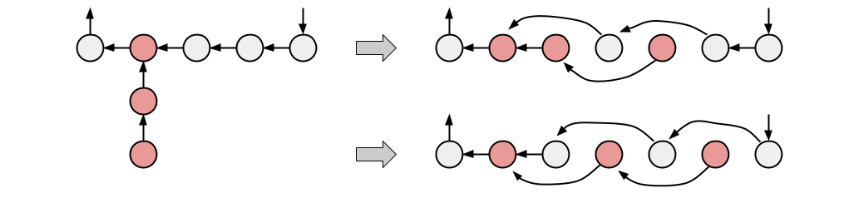
一个环上空位至多嵌入一个链上点，所以考虑可以嵌入当前链的环上边有多少条，如果比链长要短，则不存在方案；若与链一样长，则只有一种嵌入方式；若长于链，则可以有上述两种嵌入方式。于是这就完成了基环树的讨论。

剩下的部分不过是讨论一下特殊的合并情形，是简单的。

[AGC009D] Uninity

$\color{red}\texttt{[HARD]}$

感觉完全想不到/ll

首先给每个点一个权值，表示当前点是在什么时候被加入树中的（即我是在树成为第多少级的时候加入的），那么需要满足：任意两个相同权值的点之间，都必须有一个比他们权值大的点。

考虑贪心。从叶子往根贪心地选择较小的权值。考虑维护子树内一个权值的集合，表示子树内有哪些权值，能到达当前子树的根节点，且没有经过比自己更大的权值。合并两棵子树的时候，若两棵子树的这个集合有交，说明当前点权值必须 $>$ 这个交。

那么当前点就应该选择：“满足 $>$ 子树集合的交，且不在子树内集合的，最小权值”。这个贪心看起来很对，考虑证明一下。

题解的证明方法大概是，考虑子树集合中有哪些权值，将一个点的代价设置为：

$$ w(x)=\sum_{a\in S_x} M^a $$

其中 $M$ 是一个极大量。则我们可以通过比较 $w$ 的大小来比较方案的优劣（可以看作不可能进位）。而点 $x$ 的代价 $w(x)$ 应该要 $>$ 其所有儿子的 $w$ 之和，则上述方式取到的就一定是权值最小的合法解了。

维护集合不是很方便，但是根据点分治，我们知道颜色个数不会超过 $\mathcal{O}(\log n)$，因此可以用一个数来存这个集合，并使用 __builtin 函数做到 $\mathcal{O}(n)$。

[AGC009E] Eternal Average

$\color{red}\texttt{[HARD]}$

考试 $\tt{LIST}$ $2020.10.24$ $\tt{T3}$。

[AGC010D] Decrementing

$\color{red}\texttt{[HARD]}$

看到博弈问题自动爬了/px

博弈问题，首先从必败态开始反推，关注一些一步取胜态的特点。
看到一类操作复杂的博弈问题，考虑简化状态，注意操作中的不变量与必变量。

首先，必败态是显然的 1 1 1 ... 1 1 1，一步取胜态形如 k k k ... k+1 ... k k k。不过注意到实际上只有 $k=1$ 的时候才是可能的，不然另外一遍提前选一个 $k$ 进行 $-1$ 就把他破坏了。

能快速确定胜负的状态呢？可以发现当出现了 $1$ 之后，答案就只与元素和的奇偶性相关了。

一步必胜态只有 1 1 1 ... 2 ... 1 1 1，注意到此时偶数个数 $=1$，由于游戏总会结束，所以只要先手保证自己每次操作时，偶数个数都是奇数，就必胜了。注意到只要初始状态中，偶数个数是奇数，先手无论怎么样都可以保持优势，从而赢得游戏。

如果初始状态中偶数个数是偶数呢？如果不采取一些特殊措施，那么先手就会输。唯一的翻盘机会应该是：找到一个机会使得所有数字除 $2$，再来继续游戏。

注意到对于先手来说，这样的机会只有在 $>1$ 的奇数个数为 $1$ 的时候才可能出现。因此，若 $>1$ 的奇数个数 $>1$，偶数个数为偶数，则先手必败。

否则，先手一定尝试翻盘，选择唯一的 $>1$ 的奇数，将所有元素除 $2$，因此这种翻盘操作只会至多出现 $\mathcal{O}(\log V)$ 次。加上求 $\gcd$ 的复杂度，总复杂度是 $\mathcal{O}(n\log^2 V)$。

[AGC010F] Tree Game

$\color{blue}\texttt{[NORMAL]}$

从必败态开始反推。什么样是必败的？首先，当我所在点周围所有点的 $a_i$ 都 $\ge$ 我的时候，我就必败了，因为我每次移动一步，对手就可以把我赶回来，最后一定是我先走不动。

进一步，如果我走向了一个 $a_i\ge$ 我的点，对手总可以把我赶回来，这样我的 $a_i$ 减小了，可以认为“劣势”更大了。因此，我们可以得到：我不会往 $a_i\ge$ 我的点走。这件事同时能说明我不会走回头路。

于是就可以直接 $\mathcal{O}(n)$ 模拟以某一个点为根的时候，走到某一个子树，是先手必胜还是必败了。时间复杂度 $\mathcal{O}(n^2)$。

[AGC010C] Cleaning

$\color{blue}\texttt{[NORMAL]}$

鸽

[AGC011D] Half Reflector

$\color{blue}\texttt{[NORMAL]}$

十分神秘的题。

首先手玩一下，如果第一个是 A，那么就会立马被弹回去。否则，可以说明球能经过所有位置并从右侧离开。这是因为当他穿过一串 B...B，他们就全都会变成 A...A，再碰到 A 的时候，会被前面的 A 给顶回去。归纳证明。

继续观察，发现当第一个是 B 时，一次操作可以描述成将所有位置向左循环移位一次，并翻转所有点的状态。因此，可以得知每次被放到最后的字符一定是 A，在不超过 $2n$ 次操作之后，序列将变成形如 BABABA 状。

因此只需要将操作次数与 $2n$ 取 $\min$ 即可。模拟的时候使用 deque，加一个全局 $\text{reverse}$ 的 $\text{tag}$。

不过需要特判奇数的情况，此时最后会形如：只有第一个元素在 A 和 B 之间反复切换。于是只要保证最后的操作次数奇偶性与原本的相同即可。

[AGC005E] Sugigma: The Showdown

$\color{red}\texttt{[HARD]}$

首先，如果先手能走到一条边上，满足这条边两个端点在后手树上距离 $\ge 3$，我就可以无限反复横跳，输出 -1。否则，一定是走到一个后手最难追到的地方，然后等死。

不妨以两人各自的起点为各自树的根。在后手树上观察两人位置关系，注意到先手一定在后手的子树内。因为没有走到 $\ge 3$ 的地方，所以先手至多一次在后手树上向上跳两步，如果他跨出了后手的子树，则后手可以在一步内抓到他，不优。

于是，设在两棵树上点 $x$ 深度分别为 $\text{dep}_a(x)$ 和 $\text{dep}_b(x)$，则先手不能走到 $\text{dep}_a(x)\ge \text{dep}_b(x)$ 的点上，因为这样后手甚至更容易走到这个点，直接就死了。

因此只需要判断，从出发点仅走 $\text{dep}_a(x)< \text{dep}_b(x)$ 的点，能否到达一个必胜的点。如果不行，则找到能够到达的 $\text{dep}_b(x)$ 最大的点，在那里等死即可。

时间复杂度 $\mathcal{O}(n)$。