【学习笔记】图的匹配算法相关
前言
群会,我会但不完全会
本学习笔记基本参考:
【IOI2015 论文集】陈胤伯,浅谈图的匹配算法及其应用。
【IOI2017 论文集】杨家齐,基于线性代数的一般图匹配。
二分图最大匹配
匈牙利算法,懂的都懂。$\text{Dinic}$ 求最大匹配,懂的都懂。
但是我不懂,这里大致说明一下 $\text{Dinic}$ 求最大匹配的复杂度为啥是 $\mathcal{O}(m\sqrt{n})$。
首先,$\text{Dinic}$ 一开始的 $\text{BFS}$ 是 $\mathcal{O}(m)$;$\text{DFS}$ 是 $\mathcal{O}(nm)$,但是由于是单位流量,所以 $\text{DFS}$ 是 $\mathcal{O}(m)$。
对于前 $\sqrt{n}$ 轮,总复杂度是 $\mathcal{O}(m\sqrt{n})$;
对于 $\sqrt{n}$ 轮之后,由于每次 $\text{Dinic}$ 重新建分层图的时候,其 $S,T$ 的最短路径长度严格递增,所以每条增广路长度都 $\ge \sqrt{n}$。每次会把一条增广路消掉,所以至多还剩 $\sqrt{n}$ 条增广路,这里还是 $\mathcal{O}(m\sqrt{n})$。
于是最后的复杂度是 $\mathcal{O}(m\sqrt{n})$。
二分图最大匹配关键点
关键点指一定在最大匹配中的点。一个很简单的想法是每次删除这个点,重新跑一遍最大匹配,如果答案减小了,则说明该点一定在最大匹配中。但是这样太慢了,有一种更好的方法:
由于已经是最大匹配了,所以图上不存在增广路,只有交错路。我们现在只考虑左部点中的关键点(右部点类似),则对于左部点 $u$,如果存在一条从 $u$ 出发的,以匹配边开始的交错路,到达一个非匹配点 $v$,则 $u$ 不是关键点。
这是因为,将 $u\rightarrow v$ 上的边状态翻转,$u$ 就不是匹配点了。
考虑倒过来做,每次找到一个非匹配点,考虑这个非匹配点能把哪些匹配点给标记成“不是关键点”。将非匹配边定向为从左到右,匹配边定向为从右到左,则从每一个非匹配点 $\text{DFS}$ 到的匹配点都不是关键点。
由于只关心可达性,所以复杂度是 $\mathcal{O}(n+m)$。
二分图最大匹配关键边
关键边指一定在最大匹配中的边。
考虑一条匹配边 $e$,当前匹配为 $M$,若当前边不是关键边,则可以找到另一个匹配 $M'$ 使得 $e$ 不在最大匹配中。考察 $M \oplus M'$,即两者的对称差。
首先,$e$ 一定在 $M\oplus M'$ 中,又两个匹配都是最大匹配,所以一定会形成一些链、环。由于是二分图,所以一定是若干偶交替链和偶交替环。
对于偶交替链,链的一段一定是未匹配边,也就是链有一个端点是未盖点,这说明 $e$ 的两个端点中,存在一个能够通过以匹配边为开始的交替路,走到一个未盖点,这就是非关键点。因此,首先需要判断 $e$ 的两个端点是否存在非关键点。
对于偶交替环,只需要判断 $e$ 是否在一个环中即可,如果在一个交替环上,则可以通过将环上边取反使当前点变为没有被选择。于是可以将匹配边设为从左往右,未匹配边设为从右往左,跑 $\text{Tarjan}$ 缩点,即可判断。
时间复杂度 $\mathcal{O}(n+m)$。
二分图最大独立集
独立集指一个点集,集合内任意两个点之间没有连边。最大独立集指所有独立集中大小最大的。
对于一张二分图,求出其最大匹配 $M$,由于 $M$ 中边的端点不重合,且一条边两个端点至多只有一个在最大独立集中,所以最大独立集大小 $\le n-|M|$。现在给出一种方法,使得最大独立集大小 $=n-|M|$。
首先,对于一组最大匹配 $M$,所有未盖点都必须在最大独立集中,对于匹配边,两端的点恰好选择一个。每次,从已经决定是否选择的点开始,将还没有考虑的边的状态进行更新,即更新与一个已经确定状态的点相连的所有点的状态。如果没有这样的点,则随意选择一个点的状态,然后继续做。
这样会出现冲突的话,只有以下情形:
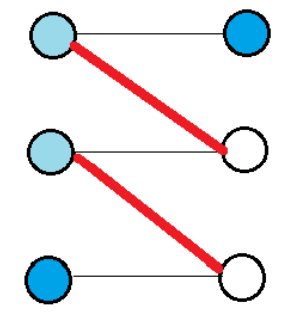
其中红色边是匹配边,深蓝点是已经选入最大独立集的未盖点。注意到这样实际上意味着出现了一条增广路,与 $M$ 是最大匹配矛盾,于是不会出现冲突。
于是,只需要每次从一个确定了状态的节点开始,更新其他点的状态即可。一个点只会被确定一次,所以复杂度是 $\mathcal{O}(n + m)$。
当然,也可以直接最小割。
二分图最小点覆盖
点覆盖指一个点集,使得任意一条边的两个端点中,都至少有一个点在该集合中。
根据定义可得,任何点覆盖的补集都是独立集,任何独立集的补集都是点覆盖。于是最小点覆盖 $=n-$ 最大独立集 $=$ 最大匹配。
二分图最小字典序完备匹配
设 $\text{match}_i$ 是二分图中与左部点 $i$ 匹配的右部点。最小字典序完备匹配要求最小化序列 $\text{match}_1,\text{match}_2...$。
套用对于这种字典序最小问题常用的贪心思想,每次考虑第一个元素最小是多少。
首先,容易说明对于两个完备匹配 $M$ 和 $M'$,其对称差一定形如若干交替环。从小到大考虑当前点的某一条边是否能加入匹配,如果这条边已经是匹配边了,显然在完备匹配中;如果这条边在一个交替环中,也可以通过将环上边取反来将当前边加入完备匹配。
判断这条边是否在一个交替环里,还是可以使用 $\text{Tarjan}$ 缩强连通分量,然后判断当前边的两个端点是否在同一个强连通分量中。
选定一组匹配之后,为了不再被影响,可以将这两个点从图中删除。容易发现剩下的部分仍然是剩下的图的完备匹配。因此复杂度是 $\mathcal{O}(nm)$。
一般图最大匹配
他来力
带花树算法
一般图问题在于有奇环,就会出现下面这种情况:
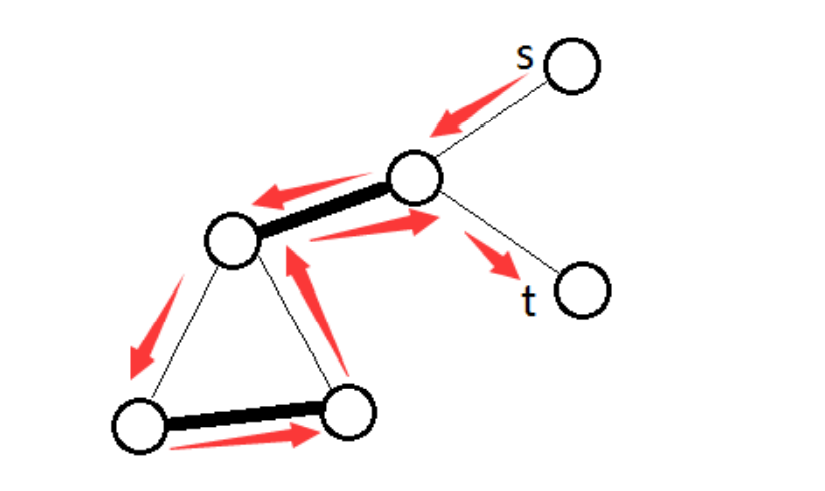
这样我绕一下奇环,走回同一条边的时候这条边的选取状态就会出现问题。于是就需要带花树了!
其主要思想就是将奇环直接缩成一个点,然后做二分图匹配的内容。具体过程是:
首先,记录 $\text{pre}$ 数组表示当前点的前驱节点是谁,找到增广路之后,将顺着前驱节点进行增广,且后续在缩环的时候对 $\text{pre}$ 的修改也是很关键的一个步骤。
从一个未盖点 $s$ 开始匹配,每次交替拓展,也就是拉出一棵交替树。将点奇偶标号,根是偶点,注意到每次选择一个奇点之后,他会自动将自己匹配的点拉进来,成为一个偶点。
设当前偶点是 $x$,枚举出点 $y$。
若 $y$ 没有被访问过:若 $y$ 是未盖点,则已经找到增广路;否则将其匹配的点拉入,继续进行。
若 $y$ 被访问过:则说明当前边是交错树的非树边。如果 $y$ 是偶点,则说明找到一个偶环,其正确性和二分图类似;否则,即若 $y$ 是奇点,说明找到一个奇环,则需要将这个环缩起来。
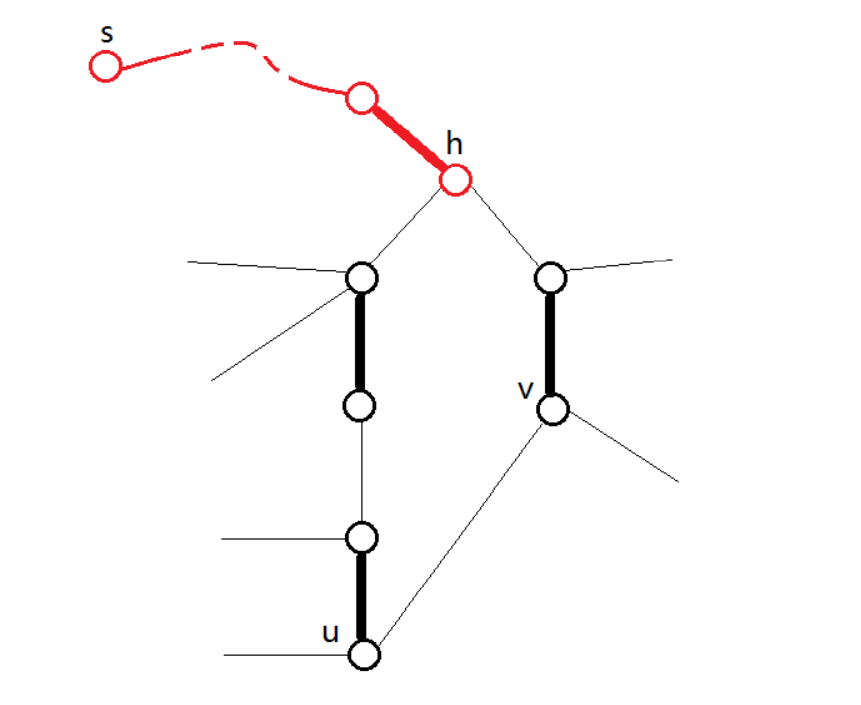
考虑这样一张图,$s$ 到 $h$ 是一条交错路,其中 $s$ 是未盖点。这里我们就找到了一个奇环。容易得出:$s$ 到 $h$ 路径上,连接 $h$ 的边一定是匹配边,且这个环上只有 $h$ 连接的两条边都是未匹配边,除了 $h$ 外从环外连向环上点的所有边都是未匹配边。
注意到不论从哪个点进入环,总有一种合法的方案能够走到 $h$,而且显然只能从 $h$ 走出去——因为只有 $h$ 与环外的边是匹配边。
于是,我们可以调整这个环上的 $\text{pre}$,使得不管从什么地方进来,都有一种方案能够引他走向 $h$。例如我们将 $\text{pre}_u$ 设置为 $v$,则当某条交替路从 $u$ 的匹配点走进环,$u$ 就会被自动拉入,然后顺着 $\text{pre}_u=v$ 从环的一侧走向 $h$。
至于找 $h$ 这个点,注意到他一定是 $u,v$ 的 $\text{LCA}$,又图一直可能变化,所以只能暴力跳父亲来找。缩点可以直接并查集。
一轮增广是 $\mathcal{O}(n^2)$,要从每个点开始增广一次,所以时间复杂度是 $\mathcal{O}(n^3)$。
基于线性代数的一般图匹配算法
完美匹配的存在性
$\text{Tuttle}$ 定理
定义无向图 $G$ 的 $\text{Tuttle}$ 矩阵是一个 $n\times n$ 的矩阵 $\tilde{A}(G)$,满足:
$$ \tilde{A}(G)_{i,j}= \left \{ \begin{matrix} x_{i,j} && (i,j)\in E,i<j\\ -x_{j,i} && (i,j)\in E,i>j\\ 0 && \text{otherwise} \end{matrix} \right. $$
其中 $x_{i,j}$ 是一个独立的变量。
$\text{Tulle}$ 定理:图 $G$ 有完美匹配 $\iff \det\tilde{A}(G)\ne 0$。
证明:
首先,一张图有完美匹配,当且仅当他可以被“偶环覆盖”,即可以通过若干偶环覆盖所有的点,使得每个点恰好在一个偶环中。构造方式很简单,只需要将偶环上的边交替选择即可。
考虑 $\det$ 的意义,实际上就是选择了一个环覆盖,如果环覆盖中存在奇环,容易发现翻转这个环后,前面的 $(-1)^{\tau(p)}$ 系数翻转,两个权值相加为 $0$。显然能构造一一对应关系,于是 $\det \tilde{A}(G)\ne 0\iff G$ 有偶环覆盖 $\iff G$ 有完美匹配。
随机化
由于 $\text{Tuttle}$ 矩阵中有很多个变量,所以直接求解行列式显然是不够快的。注意到我们只需要知道 $\det \tilde{A}(G)$ 是否为 $0$ 即可,而 $\det \tilde{A}(G)$ 实际上是一个 $m$ 元多项式 $P(x_1,x_2,\cdots x_m)$,则我们的目标就是判断 $P$ 是否恒为 $0$。
简单的想法是给每个变量随机一个权值,看其取值是否为 $0$,从而判断 $P$ 是否恒为 $0$。这个事情的正确性可以通过以下引理说明:
$\text{Schwartz-Zippel}$ 引理:对于域 $\mathbb{F}$ 上一个不恒为 $0$ 的 $n$ 元 $d$ 度多项式 $P(x_1,x_2,\cdots x_n)$,设 $r_1,r_2,\cdots r_n$ 是 $n$ 个在 $\mathbb{F}$ 中独立选取的随机数,则:
$$ \text{pr}[P(r_1,r_2,\cdots r_n)=0]\le \dfrac{d}{|\mathbb{F}|} $$
可以简单理解为,如果这个多项式不恒为 $0$,则随机选到一些变量,导致多项式取值为 $0$ 的概率很小。具体证明可以归纳 但是我鸽了。
我们知道,$\det \tilde{A}(G)$ 的度是 $\mathcal{O}(n)$ 级别的,所以只需要选取 $\mathcal{O}(n^2)$ 级别的质数 $p$,在 $\bmod p$ 意义下进行上述过程,其错误概率 $\le \dfrac{1}{n}$。当然,可以多随几次来提高正确率。