【学习笔记】Lyndon 分解

前言

群除我会了或者即将会了

鸽了 $100$ 年终于来学了。

本学习笔记基本参考【IOI2021 论文集】胡昊，浅谈 $\text{Lyndon}$ 分解。
还有这里。

$\text{orz huhao}$

定义

对于字符串 $S$，称其为 $\text{Lyndon}$ 串当且仅当 $S$ 严格 $<$ 其所有后缀。

称字符串 $S$ 的 $\text{Lyndon}$ 分解为：将字符串划分为若干子串 $A_1A_2\cdots A_k$，满足 $\forall i$，$A_i$ 是 $\text{Lyndon}$ 串，且 $A_i\ge A_{i+1}$。

前置证明

$S$ 是 $\text{Lyndon}$ 串 $\iff$ $S$ 是其所有循环同构中字典序严格最小的。

注意上述定义中给出的是严格小于所有后缀。证明没太看懂，到时候再补

若 $Sa$ 是某个 $\text{Lyndon}$ 串的前缀，其中 $S$ 是字符串， $a$ 是某个字符；则对于 $b>a$，$Sb$ 是 $\text{Lyndon}$ 串。

对于 $S$ 一个后缀 $T$，有 $Sa<Ta$。考虑两个串第一次不一样的位置 $p$，若在 $|Ta|-1$ 及以前，则不改变大小关系；若恰好是 $|Ta|$，则将 $a$ 替换成 $b$ 也不改变大小关系。

若 $S,T$ 都是 $\text{Lyndon}$ 串且 $S<T$，则 $ST$ 是 $\text{Lyndon}$ 串。

若 $|S|\ge |T|$，则 $ST<T$，又 $S,T$ 分别是 $\text{Lyndon}$ 串，所以所有 $T$ 的后缀都 $> T$。

若 $|S|<|T|$，分类讨论一下。若 $S$ 不是 $T$ 的前缀，则显然 $ST<T$；若 $S$ 是 $T$ 的前缀，考虑反证：若 $ST$ 不是 $\text{Lyndon}$ 串，则 $ST>T$，这说明 $T_{|S|+1...n}<T$，与 $T$ 是 $\text{Lyndon}$ 串矛盾。因此证毕。

$\text{Lyndon}$ 分解存在且唯一。

存在性：

一开始设 $S$ 是 $n$ 个长度为 $1$ 的串 $s_1s_2s_3\cdots s_n$，则每次只需要找两个 $s_i<s_{i+1}$，将其合并为一个部分就行了。

唯一性：

反证，假设存在两种 $\text{Lyndon}$ 分解：

$$ S=A_1 A_2\cdots A_i A_{i+1}\cdots A_k $$

$$ S=A_1 A_2\cdots A_i A'_{i+1}\cdots A'_{k'} $$

不妨设 $|A_{i+1}|<|A'_{i+1}|$。设 $A'_{i+1}=A_{i+1}A_{i+2}\cdots A_{m_{1...p}}$，则：

$$ A'_{i+1}<A_{m_{1...p}}\le A_m<A_{i+1} $$

又 $A_{i+1}$ 是 $A'_{i+1}$ 的前缀，所以矛盾。

一个 $\mathcal{O}(n\log n)$ 的算法

设 $a_i$ 表示 $i$ 之后，第一个位置 $j$ 使得 $S_{i...n}>S_{j...n}$，若不存在，则设 $a_i=n+1$。

则 $S$ 的 $\text{Lyndon}$ 分解的第一项是 $S_{1,a_1-1}$，后面的项就是 $S_{a_1,n}$ 的 $\text{Lyndon}$ 分解。

由于要比较后缀的大小关系，所以需要使用 $\text{Suffix Array}$，复杂度 $\mathcal{O}(n\log n)$。

注意到，此算法可以得到所有后缀的 $\text{Lyndon}$ 分解。

$\text{Duval}$ 算法

$\text{Duval}$ 算法可以在 $\mathcal{O}(n)$ 的时间复杂度内求出一个串的 $\text{Lyndon}$ 分解。其主要思想就是将字符串 $S$ 划分为三部分 $S_1,S_2,S_3$，分别表示已经划分完毕的部分，正在划分的部分，和还未考虑的部分。

其中 $S_2=t^m+v$，其中 $t$ 是一个 $\text{Lyndon}$ 串，$v$ 是 $t$ 的一个前缀。

现在建立三个指针 $i,j,k$，$i$ 指向 $S_2$ 的第一个字符，$k$ 指向 $S_3$ 的第一个字符，$j$ 指向 $k-|t|$，即上一个循环节中 $k$ 的对应位置。

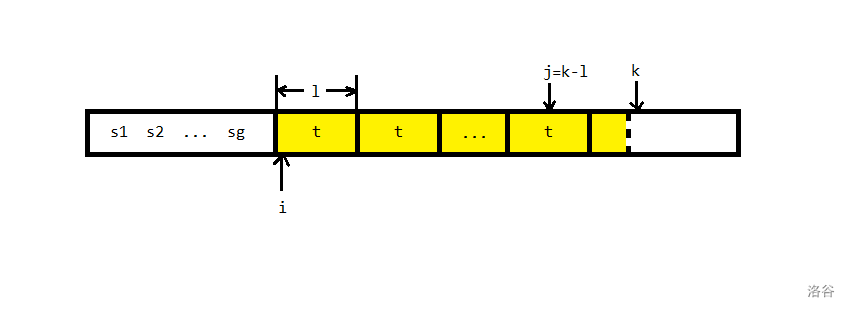
• 若 $s_k=s_j$，则循环节可以继续延申，$j\leftarrow j+1,k\leftarrow k+1$。
• 若 $s_k>s_j$，根据上述结论，$v+s_k$ 是一个 $\text{Lyndon}$ 串。由于要满足递减的条件，所以 $v+s_k$ 要一直往前合并，最后会组成 $t^m+v+s_k$ 为一个新的 $\text{Lyndon}$ 串。即 $j\leftarrow i,k\leftarrow k+1$。
• 若 $s_k<s_j$，则我们称 $t^m$ 的部分的 $\text{Lyndon}$ 分解已经被确定，将 $m$ 个 $t$ 串加入 $S$ 的 $\text{Lyndon}$ 串，从 $v$ 的开头开始继续分解。

注意到，此算法可以得到所有前缀的 $\text{Lyndon}$ 分解。

几个问题

为啥是 $\mathcal{O}(n)$？

$i,k$ 是递增的，$j$ 的移动次数不超过 $k$，故是 $\mathcal{O}(n)$。

为啥这样分解出的 $\text{Lyndon}$ 串字典序不增？

考虑每次从 $S_2$ 中放入 $S_1$ 中需要满足什么条件。首先 $v$ 是 $t$ 的前缀，且最新的字符 $s_k<s_j$，则我们会在 $S_1$ 中放入若干 $t$。由于 $j,k$ 是 $t$ 的对应位置，所以一定有 $v+s_k<t$，故字典序不增。