趣味简单题

题目链接：CF1301D 【Time to Run】

题意简介：

给定一个 $n \times m$ 的矩阵，相邻的两个格子之间有两条方向相反的有向边，长度均为 $1$，从左上角开始，每次可以向左、右、上、下走一格，但是不能重复走已经走过的路（可以重复经过到过的格子，不能走出网格图），问是否可能走出一条长度为 $k$ 的路径（不一定要在左上角结束），如果可以，需要输出方案。

$n,m \le 500$

这题一开始想，还以为是个什么欧拉路的题目，但是输出方案的方式给了我们提示...

输出方案最多 $3000$ 行，每一行一个数字 $f,f \le 10^9$ 和一个长度不超过 $4$ 的字符串。

字符串中使用字符 $L,R,U,D$，分别代表向左、右、上、下走一步。

$f$ 则意为重复按照字符串所说地走 $f$ 次。

这个输出方法很玄学，如果是我们找到了一种走法，再去考虑输出方案，显然我们还需要分割路径的字符串，这很麻烦。

所以考虑构造一种万能走法，能够囊括 所有的长度。

注意标黑的部分，那显然我们如果能找到一种走法，使得每一条边都能被遍历，显然就是最优的了。

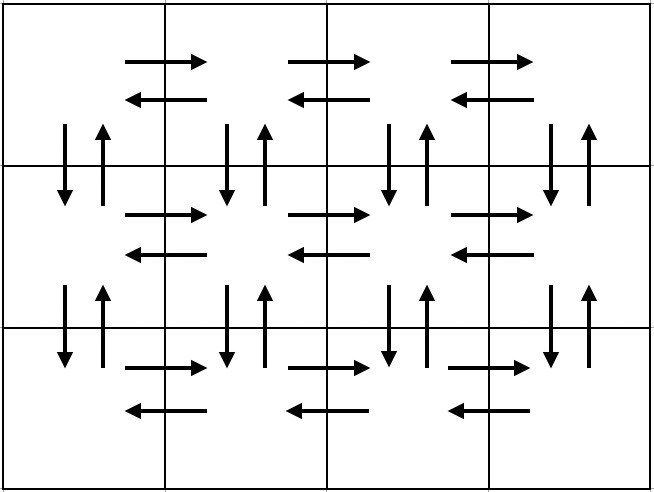
我们令左上角为 $(1,1)$ 第一行第二个为 $(1,2)$ 以此类推

我们很快可以找出一种走法，可以遍历完第一行格子之间的边，和第一行与第二行之间的所有边的走法（除了 $(2,1)$ 到 $(1,1)$ 一条）

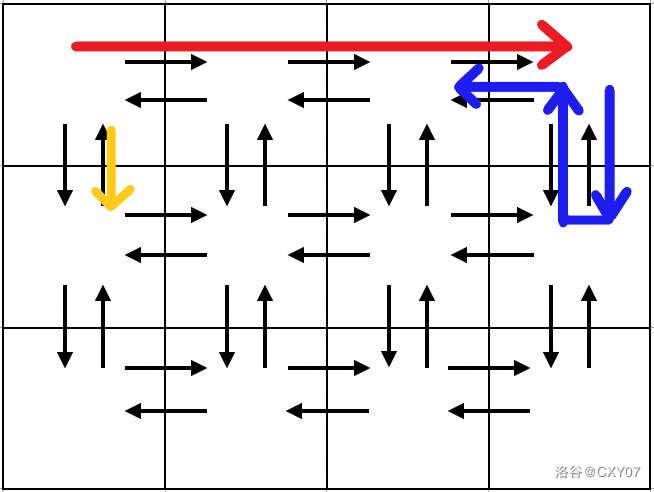
这中间蓝色显然是可以重复走的 懒得画了，红色是 $R$ 重复，蓝色是 $DUL$ 的重复，黄色是一个 $D$，这样显然，第二行也可以用相同的走法，从而到达了第三行......以此类推

注意一下最后一行只能 $R$ 之后 $L$ 回来，不能走蓝色那种了，因为它没有下一行了，特判一下即可

最后，我们会到达 $(n,1)$ ，不难发现所有 $(i,1)$ 到 $(i-1,1)$ 的路径都是没走过的，那我们就一直 $U$ 上去即可。

那这种做法是否符合输出规范呢？

显然处理一行，我们需要的行数为 $3$ : 红色一行，蓝色一行，黄色一行

$n_{max} = 500$ ，所以大约需要 $1500$ 行的样子，显然 $1500 < 3000$，所以行数限制是没问题的。

再来看字符串长度问题，根据上面所说，我们只会走 $R,DUL,D,U,L$ 这 $5$ 种字符串，显然长度没有超过 $4$ ，这个限制也没有问题

再有 $f$ 的限制$(f\le 10^9)$，回想一下，我们的走法都在一行或者一列里面走，循环次数显然不会超过 $max(n,m)$ 那肯定就不会超过 $10^9$ 啦

那么我们就做完了。

注意特判 $m=1$ 的情况！ 为什么？

因为我们的走法第一步就是 $R$ ，但是 $m=1$ 时，我们没有 $R$ 的余地！

所以特判一下直接 $D$ 再 $U$ 就好了

注意每走一步新的都要判断是否在这一步中结束，因为他要最先输出命令行数，所以我就把它丢到 $vector$ 里面了，两个 $vector$ 分别存放的是 $f$ 和对应的字符串，应该不难理解。

$Code:$

#include<bits/stdc++.h>
using namespace std;

int n,m,savk,k,lim;
vector<int> cnt;
vector<string> ans;

inline void print() {
    puts("YES");
    int len = cnt.size(),tmp;
    cout << len << endl;
    for(register int i = 0;i < len; ++i) {
        cout << cnt[i] << ' ' << ans[i] << endl;
        tmp += cnt[i] * ans[i].length();
    }
    return;
}//输出答案

int main () {
    //freopen("in.in","r",stdin); 
    cin >> n >> m >> k; savk = k;
    if(k > 4 * n * m - 2 * n - 2 * m) {puts("NO"); return 0;}//总共边数都没有这么多
    if(m == 1) {//特判
        lim = n - 1;
        if(k <= lim) {
            cnt.push_back(k),ans.push_back("D");
            k = 0;
            print();
            return 0;
        }// D下去
        k -= lim;
        cnt.push_back(lim),ans.push_back("D");
        if(k <= lim) {
            cnt.push_back(k),ans.push_back("U");
            k = 0;
            print();
            return 0;
        } 
        k -= lim;
        cnt.push_back(lim),ans.push_back("U");// U上来
        if(!k) print();
        else puts("NO");
        return 0;
    }
    lim = m - 1;//指红蓝两种走法最多走多少次，显然是m-1
    for(register int i = 1;i <= n; ++i) {
        if(k <= lim) {
            cnt.push_back(k),ans.push_back("R");
            k = 0;
            break;
        }
        k -= lim;
        cnt.push_back(lim),ans.push_back("R");//红
        if(i < n && k <= lim * 3) {//不是最后一行并且在这一步中结束
            int tmp = k / 3,_;
            if(tmp) {
                cnt.push_back(tmp),ans.push_back("DUL");
            }
            _ = k - tmp * 3;
            if(_ == 1) cnt.push_back(1),ans.push_back("D");
            else if(_ == 2) cnt.push_back(1),ans.push_back("DU");
            k = 0;//蓝中间结束，注意最后一下是 D 还是 DU
            break;
        }
        if(i < n) {//不是最后一行的情况
            k -= lim * 3;
            cnt.push_back(lim),ans.push_back("DUL");
            cnt.push_back(1),ans.push_back("D");//蓝
            k--;
        } else {//最后一行，直接L回去
            if(k <= lim) {
                cnt.push_back(k),ans.push_back("L");
                k = 0;
                break;
            } else {
                k -= lim;
                cnt.push_back(lim),ans.push_back("L");
            }
        }
        if(!k) break;
    }
    if(!k) {//如果走完了，输出
        print();
        return 0;
    }
    if(k <= n - 1) {//否则我们可以走 U n-1次
        cnt.push_back(k),ans.push_back("U");
        print();
    } else puts("NO");//肯定就不行了
    return 0;//End.
}

趣味题，作为一道 $Div2$ 的 $D$，有种让人耳目一新的感觉 (主要是可以上分了)，注意特判，就没什么难的了。

初三的 $OIer$，请多关照